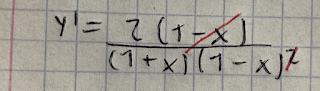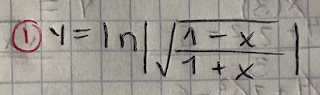Portada

Escuela Preparatoria Oficial Anexa a la Normal de Cuautitlán Izcalli 

Grado: 3 Grupo 4 Turno Vespertino

Matemáticas 

Profesor: Jorge Iván Velázquez Miranda  

BLOG MATEMATICO

Hernández Serna Omar

Hernández Martínez Rodrigo

Lazo Arcivar Erika Mariel

García Alcántara Eder

Zarza Dorantes Ángel Uriel

Concepto Limites

El limite matemático es la aproximación hacia un valor determinado. Es un valor que no puede considerarse porque genera indeterminación la mayoría del tiempo.

 

Video Limites conceptos básicos

Propiedades de los Limites

Limites Determinados

El limite determinado se puede presentar de forma lineal y en forma de cociente, un limite en forma de cociente. Se sabe que es determinado cuando al sustituir el valor de "x" en la función, el resultado del denominador es diferente a 0.

Por ejemplo:
a)Lim: x+1
x=5

Paso 1
Se sustituye el valor de "x" en nuestra función

Lim: (5)+1
x=5

b)Lim:  x²- 4/x+2
x=2

Paso 1
Se sustituye x en la función

Lim= (2)²- 4/(2)+2
x-2

Paso 2
Corrobora que es indeterminado o determinado resolviendo la función

Lim:   (2)²- 4/(2)+2= 4-4/2+2= 0/4= 0

Ejemplo 2:

Limites Indeterminados

Este limite se presenta, cuando el limite en la parte del cociente, al sustituir la "x" nos da 0 (error matemático), entonces procedemos a factorizar los elementos que podamos.

Factorización

Una vez que compruebes que tu limite es indeterminado, analiza la función como el ejemplo siguiente

Lim:   x²-16/x-4
x=4

Paso 1

Factoriza lo que puedas, en este caso se puede factorizar el numerador de la función 

Lim:   x²-16/x-4= (x-4)(x+4)/x-4
x=4

Paso 2

Analiza si puedes simplificar el limite, aquí se presentan bases iguales, divídelas

Lim:   (x-4)(x+4)/x-4 = x+4
x=4

Paso 3

Sustituye el valor de x y ese será tu resultado

Lim:   (4)+4=8

x=4

Factorización por factor común

Si en tu ecuación hay varios términos semejantes con algún termino en común, se puede resolver por factor común; ejemplo:

Lim:    x²+4x-6x/4x 

x=0

Paso 1

Determina el factor en común de la función 

Lim:    x²+4x-6x/4x= x(x+4-6)/x(4)

x=0

Paso 2

Se eliminan los términos semejantes, en este caso las x fuera de los paréntesis y queda así:

Lim:     x(x+4-6)/x(4)= x+4-6/4

x=0

Paso 3 

Ahora resuelve sustituyendo el valor de la x en tu función, y simplifica lo que se pueda

Lim:   (0)+4-6/4= -2/4= -1/2

x=0

Factorización por diferencia de cubos y suma de cubos

Cuando hay una ecuación que este elevada al cubo, se tiene que resolver por una formula, puede ser por suma de cubos o diferencia de cuadrados:

Diferencia de cubos:   (a³-b³)=(a-b)(a²+ab+b²)

Suma de cubos:  (a³+b³)=(a+b)(a²-ab+b²)

Ejemplo diferencia de cubos

Lim:  x³-1/x-1

x=1

Paso 1

Sustituir por medio de la formula la ecuación elevada al cubo

Lim:   x³-1/x-1=  (x-1) (x²+(x)(1)+1²)/x-1

x=1 

Paso 2 

Simplificar lo que se pueda y contrarrestar los términos semejantes del numerador y denominador

Lim:   (x-1) (x²+(x)(1)+1²)/x-1= x²+x+1²

x=1

Paso 3

Sustituye el valor del limite en las variables de la ecuación 

Lim:    (1)²+1+1² 

            1+1+1= 3

x=1

Ejemplo suma de cuadrados 

Para la suma de cuadrados, es el mismo procedimiento pero se cambian los signos de toda la formula 

Lim:    x³-8/x²-4

x=2

Paso 1

Sustituye la función a como te indica la formula 

Lim:   x³-8/x²-4= x³-2³

x=2    (x-2)*(x²-2x+2²)/x²-4

Paso 2

Se resuelve y factoriza lo que se pueda resolver dentro y fuera de los paréntesis, y después, se dividen los términos semejantes del numerador y denominador.

Lim:   (x-2)*(x²-2x+2²)/(x-2)(x+2)=

x=2      x²-2x+2²/x+2

Paso 3 

Sustituir el valor de x en la operación y resolverla 

Lim:   (2)²-2(2)+2²/(2)+2= 

x=2     4-4+4/4=  1

Limites con raíz y doble raíz

Raíz

Este método se puede aplicar cuando en tu limite, ya sea en el numerador o denominador, hay una raíz cuadrada como el ejemplo siguiente

Lim:   √x-1/x-1

x=1

Paso 1

Repetir los términos que tienen raíz en un paréntesis que indica multiplicación, pero se le cambia el signo que opera a las raíces

Lim:   √x-1/x-1*(√x+1/√x+1)

x=1

Paso 2

Multiplicar los términos semejantes de la ecuación 

Lim:   √x²-1/(x-1)(√x+1)

x=1

Paso 3

Cancelar las potencias con las raíces en caso de que tengan el mismo exponente

Lim:    x-1/(x-1)(√x+1)

x=1

Paso 4

Simplificar o dividir los términos semejantes del numerador y denominador

Lim:   1/√x+1

x=1

Paso 5

Simplificar y sustituir el valor de x en las variables de la ecuación y resolver hasta su mínima expresión

Lim:   1/√x+1= 1/√1+1= 1/2

x=1

Doble Raíz

Este se presenta cuando en el numerador y en el denominador está presente una o mas raíces

Lim:   √x-2/√4x-4

x=4

Paso 1

Repite las raíces en un paréntesis y multiplícalo por la función

Lim:   √x-2/√4x-4: (√x+2/√x+2)(√4x+4/√4x+4)

x=4

Paso 2

Multiplica los términos semejantes  

Lim:   √x-2/√4x-4: (√x+2/√x+2)(√4x+4/√4x+4)= (√x²-4)(√4x+4)/(√4x²-16)(√x+2)

x=4

Paso 3

Se eliminan las raíces que están elevadas al cuadrado y factoriza lo que se pueda

Lim:    (√x²-4)(√4x+4)/(√4x²-16)(√x+2)= (x-4)(√4x+4)/4(x-4)(√x+2)

x=4

Paso 4 

Divide los términos semejantes de la función 

Lim:   (x-4)(√4x+4)/4(x-4)(√x+2)= √4x+4/4(√x+2)

x=4

Paso 5

Por último, sustituye el valor de "x" en las variables de la función, resuelve y simplifica lo mas que se pueda

Lim:  √4(4)+4/4(√(4)+2)= √16+4/4(2+2)= 8/16= 1/2 

x=5

Limites que tienden al Infinito

Este caso de limite se da cuando el valor del mismo "x" tiende al infinito, el resultado va a varear dependiendo de lo que obtengas como se puede dar en los siguientes casos.

Reglas

a)0/k=0    b)k/0=∞    c)∞/k=∞    d)k/∞=0    e)∞/0=∞    f)0/∞=0

Resolvamos un ejercicio para ver como es que se aplica

Lim      x³-1/x²+4

x=∞

Paso 1

Una vez que identifiques que tu limite tiende al infinito, en la función vas a identificar la variable con la potencia máxima, una vez identificado, cada uno de los elementos de tu función va a ser divididos por este elemento.

Lim      x³-1/x²+4=  x³/x³-1/x³:/:x²/x³+4/x³

x=∞

Paso 2

Vas a simplificar las expresiones que se puedan

Lim:     x³/x³-1/x³:/:x²/x³+4/x³= 1-1/x³:/:1/x+4/x³

x=∞

Paso 3 

Sustituye el valor de la "x" en las variables de tu limite 

Lim:   1-1/∞³:/:1/∞+4/∞³

x=∞

Paso 4

Eleva tus infinitos e elimina el exponente. Una vez hecho esto, identifica si estás cumpliendo alguna de las reglas que están al inicio de la pagina. Si es así cámbialas por su respectivo valor

Lim:    1-1/∞:/:1/∞+4/∞= 1-0/0+0

x=∞

Paso 5 

Resuelve la operación final y verifica si el resultado cumple con algunas de las reglas. Cambia su valor dependiendo de cuál se cumpla 

Lim:   1-0/0+0= 1/0= ∞

Te dejamos unos videos para que puedas aclarar mas la información 

Introducción limites al infinito                                                                                                             

 

Ejemplos 

Concepto Derivadas

La derivada es el resultado de un limite, representa la pendiente de la recta tangente en la gráfica.

Una derivada también puede ser la velocidad con la que se mueve una función según cambie el valor de su variable independiente

Características 

*Pendiente

*Razón de cambio 

*Rapidez con la que se modifica una función

Da click en la imagen para mas información

Reglas de las derivadas

Función constante 

La formula se puede expresar de la siguiente forma 

Y=K o F(x)= K o F'(x)=Y'

La derivada de una función constante siempre va a ser igual a 0

Función lineal

La derivada de una función lineal va a ser el numero que acompaña a las variables.

y= ax+b o F(x)= ax+b

Función con potencia

y=un

"u" es = a cualquier función 

n=potencia 

y'=n*u^n-1

El exponente que acompaña a la “x” baja a multiplicar al término que acompaña a la variable y al exponente se le resta 1

Regla de la cadena(binomio elevado a una potencia)

y=(2-3x)⁵

Se hace uso de la regla de producto, donde el exponente baja del lado izquierdo del paréntesis y se copia de nuevo la función pero al exponente se le resta 1. Después se deriva lo que esta dentro del paréntesis. Por ultimo se multiplica la derivada por el termino independiente 

Regla del Producto

y=u*v

y'= u'v+uv' 

Se utiliza cuando 2 funciones se están multiplicando entre si, y para resolver la función se tiene que seguir la regla que indica los siguientes pasos:

Derivar "u" y copiar "v"

Colocar signo de mas

Copiar "u" y derivar "v"

Regla del Cociente 

y=u/v

y'=u'v-uv'/v²

De igual manera, organiza de acuerdo a la fórmula

Derivar "u" y copiar "v"

Colocar signo de menos

Copiar "u" y derivar "v"

Y todo eso se divide entre v²

Raíz

y=√u                      

y'=u'/2√u    

Siguiendo los pasos de la formula, se saca la derivada de "u" y esta se divide entre 2 veces la raíz de "u"

Raíz cúbica en adelante 

y=k√u 

y'= u'/k*k√u^k-1

Cuando la raíz no es cuadrática y es cúbica en adelante, la formula que la "u" se derive, se divida entre el numero de la raíz por la raíz del mismo numero. Después se va a copiar la función dentro de la raíz y se va a elevar al numero de la constante menos 1

Raíz con cociente

Cuando la función esta en forma cociente y todo dentro de una raíz, se aplica la siguiente formula.

Para este tipo de función tenemos que aplicar 2 reglas, la del cociente y raíz, donde la predominante es la regla de la raíz. 

Logarítmica

y=ln: lul    

y'= u'/u

Lo que indica esta regla es que tenemos que derivar nuestra función y dividirla sobre la función natural

Logarítmica con cociente 

y= ln: lu/vl

y'= u'v-uv'/v²/u/v

Para esta formula vamos a aplicar 2 reglas, la del cociente y logaritmo. Y lo único que hay que hacer es sustituir nuestra función conforme lo que nos indica la regla. 

Logarítmica con raíz y cociente 

En esta función vamos a utilizar 3 reglas de la derivación, la de la raíz, la del cociente y la logarítmica. Como se ve en la formula la "u" es lo que esta en el numerador, y la "v" es lo que esta en el denominador. lo que se tiene que hacer es sustituir los valores de la función en la formula.

Video de apoyo

Aplicación de Derivadas (constante, lineal, potencia)

Constante

Siguiendo las reglas de derivación se resolverán algunos ejemplos de derivadas 

a)  y=4                       b)  y=7                c)  y=7+5+6             d)  y=2-7

     y'=0                            y'=0                    y'=0                          y'=0

Lineal

Aplicando la regla, el resultado de derivar una función lineal es, el numero que acompaña a la variable y la variable se elimina.

a)  y=2x+1            b)  y=-x+4          c)   y=3/2x + 1         d)   y= 2-3x

     y'=2                      y'= -1                    y'= 3/2                     y'=-3

Potencia

Se multiplica la constante por el exponente y se resta 

a)  y=7x⁵            b)   y=x³         c)   y=x⁵       d)   y=9x²

     y'=35x⁴                y'=3x²            y=5                y'=18x

Potencia (más de un elemento) 

 

Aplica la formula de la potencia de mas de un elemento

a)  y=(2x+1)⁵               b)  y=(x³-2x²+4x)⁴

   y'=5(2x+1)⁴(2)                y'=4(x³-2x²+4x)³(3x²-4x+4)

   y'=10(2x+1)⁴                   y'=(12x²-16x+16) (x³-2x²+4x)³

Aplicación Derivadas(cociente, producto, raíz)

 Cociente

Paso 1: Como la regla indica se tiene que derivar "u"(1-x), el resultado de eso es -1, se añade "v"(1+x). Después se resta "u"(1-x) y esto se multiplica por la derivada de "v"(1+x) que da como resultado 1: y en la parte del denominador se eleva al cuadrado "v"(1+x).

Paso 2: Resuelve las operaciones que se puedan en el numerador, al resolverlo uno de los elementos se eliminara; simplifica los términos semejantes que son (-x), (x), lo que sobra se opera y se queda en el numerador. Poner v elevada al cuadrado como denominador.

Paso 3: Simplifica lo mas que se pueda  

Producto

y=(1-x) (1+x)

Paso 1

La formula del producto indica que hay que derivar "u" (1-x), copiar "v", indicar el signo +, copiar "u" y derivar "v"(1+x)

y=(1-x) (1+x)= (-1)(1+x)+(1-x)(1)

Paso 2

Multiplica el término independiente por "v", y después multiplica el otro término independiente con "u"

 y=(-1)(1+x)+(1-x)(1)= -1-x+1-x

Paso 3

Resuelve la operación

y= -1-x+1-x=-2x 

En el caso del producto pueden existir mezclas de funciones, solo debes de seguir los pasos para derivar y aplicarlos en la función que te pidan, aquí algunos ejemplos:

Raíz

y= √4x²

Paso 1

Siguiendo los pasos de la formula, el primer paso es derivar el valor de "u", divídelo entre 2 veces la raíz de "u"

y= √4x² 

y'= 8x/2√4x²

Paso 2

Simplifica lo que mas se pueda del denominador y numerador y lo que no se pueda se copia igual 

y'=  8x/2√4x² 

y'=  4x/√4x²

Raíz cubica en adelante 

y= 4√2x

Como se observa, aquí la raíz es cuarta, pero se opera conforme a la misma formula, solo que el valor de la constante va a ser el valor que tenga la raíz

y= 4√2x 

y'= 2/4 4√(2x)³

y'= 1/24√(2x)³

Raíz con cociente

Paso 1

Derivar "u", copiar "v", restar el valor de "u" y multiplicarlo por la derivada de "v". Colocar como cociente el valor de "v" al cuadrado. Después vamos a aplicar la regla de la raíz, entonces, colocamos el valor de la raíz que es 2 y lo multiplicamos por toda la función inicial 

Paso 2

Resuelve las operaciones que estén en el numerador  para eliminar los paréntesis. copia lo que no se pudo operar de la misma manera.

Paso 3

Aplicar la ley del sándwich, multiplicando extremos por extremos 

Paso 4

Divide lo que se pueda,(utilizando el algebra) del numerador y del denominador, lo que no se pueda dividir, se copia igual

 

    

Paso 5

Aplica la ley de los radicales para pasar de raíz a potencia en los términos semejantes, el exponente fraccionario del numerador se va a restar con el del denominador, el residuo se pone arriba o abajo dependiendo si es mayor o menor.

Paso 6 

En la parte del denominador todavía hay cosas que simplificar, en este caso como la potencia que está dentro de la raíz es mayor a la de la raíz, se puede descomponer en dos factores para que la potencia no sea mayor a la de la raíz y queda así.

 

Aplicación derivadas logarítmicas

 Logarítmicas

Paso 1

Derivar la función y dividirla entre el valor de la función, simplifica lo que se pueda hasta su mínima expresión 

a) y= ln lxl         b)  y= ln lx³l        c)  y= ln lx+1l    

   y'= 1/x                  y'= 3x²/x³             y'= 1/x+1

                                y'= 3/x

Logarítmica con cociente 

Paso 1

Como se aplican las reglas del cociente y logaritmo, el primer paso es derivar el numerador "u", copiar "v", colocar el signo -, copiar "u" y derivar "v", todo esto se divide entre "v" al cuadrado. Después se aplica la regla del logaritmo y se copia "u" debajo de todo eso.

Paso 2

Resuelve las operaciones para eliminar los paréntesis y para que sea posible eliminar un término.

Paso 3

Aplicar la ley del sándwich, multiplicar extremos por extremos. Seguido de esto, divide los términos semejantes para que se puedan contrarrestar.

Paso 4

Ya divididos los términos semejantes, en el denominador se pueden multiplicar los binomios. Y ese es el resultado final 

       

Logaritmo con raíz y cociente  

Paso 1

Aquí se aplican 3 reglas, la del cociente, la de la raíz, y la del logaritmo, por lo tanto, el primer paso es, derivar "u", copiar "v", colocar el signo -, copiar "u" y derivar "v", y todo eso se divide entre "v" al cuadrado. Después aplica la regla de la raíz, por lo que todo eso se divide entre 2 veces la raíz de "u" sobre la raíz de "v". Después se aplica la regla del logaritmo y por esto se copia la función de forma suspendía ya que no afecta en este primer paso.

Paso 2

Resolver y eliminar los paréntesis del primer numerador y operar los términos semejantes, y copia lo que no se pudo resolver.

Paso 3 

Después aplicarás la ley del sándwich, multiplicando extremos por extremos ignorando la parte logarítmica "u" ésta se copiará sin alterar nada 

Paso 4

Vuelve a aplicar la ley del sándwich, multiplicando extremos por extremos.

Paso 5

Multiplicar los términos semejantes y eliminar potencias con raíces en caso de que sean del mismo grado

Paso 6

Dividir los términos independientes del numerador y denominador 

Paso 7

Contrarrestar los paréntesis con términos semejantes en el numerador y denominador, y dependiendo del resultado, el residuo, se queda arriba o abajo. 

Paso 8

Por ultimo multiplica los binomios del denominador

                    

Concepto

Es el proceso matemático de encontrar el ritmo al cual una función trigonométrica cambia respecto de la variable independiente; es decir, la derivada de la función

Las funciones trigonométricas más habituales son las funciones sen(x), cos(x) y tan(x).

Formulario

 Existen 6 funciones principales dentro de la trigonometría, la de Sen, Cos, Tan, Csc, Sec y Cot, y cada razón trigonométrica tiene una formula para derivarla:

Derivada del Seno:

Derivada Coseno:

Derivada Tangente: 

Derivada Secante.

Derivada Cosecante:

 

Derivada Cotangente:

Identidades Trigonométricas

 Reciprocas 

Pitagóricas 

Cociente

Derivadas Trigonométricas(producto y cociente)

 Producto

Para resolver una derivada trigonométrica, que esta representada en forma de producto se debe usar la formula del producto( u'v+uv').

Ejemplo

Paso 1:

Siguiendo la formula del producto, deriva el valor de "u" y multiplícalo por el valor de tu "v", coloca el signo correspondiente, copia el valor de "u" y multiplícalo por la derivada de "v".

Paso 2:

Una vez ya derivado, utiliza las identidades reciprocas para convertir en Sen y Cos todo lo que sea posible para facilitar el trabajo.

Paso 3:

Una vez que ya intercambiaste a Sen y Cos resuelve y reduce las operaciones posibles.

Paso 4:

Si es posible y tu operación te lo permite, simplifica a la mínima expresión 

Cociente

Si tu formula esta expresada en forma de cociente, debes de hacer uso de su formula,(u'v-uv'/v2)

Ejemplo

Paso 1:

Deriva el valor de "u" y multiplícalo por el valor de "v", coloca el signo correspondiente, copia el valor de "u" y multiplícalo por la derivada de "v", todo esto sobre el valor de "v" elevada al cuadrado 

Paso 2:

Utilizando las identidades reciprocas, intercambia los valores que se puedan a Sen y Cos. Una vez que ya intercambiaste los valores, identifica y si tu función lo permite factoriza por factor común el numerador.

Paso 3:

Analiza la operación, en este caso dentro de la factorización utiliza la identidad pitagórica para cambiar el valor a su mínima expresión 

Paso 4:

Ya por ultimo paso, resuelve tu operación para simplificarla lo mas posible