Logarítmicas
Paso 1
Derivar la función y dividirla entre el valor de la función, simplifica lo que se pueda hasta su mínima expresión
a) y= ln lxl b) y= ln lx³l c) y= ln lx+1l
y'= 1/x y'= 3x²/x³ y'= 1/x+1
y'= 3/x
Logarítmica con cociente
Paso 1
Paso 2
Resuelve las operaciones para eliminar los paréntesis y para que sea posible eliminar un término.
Paso 3
Aplicar la ley del sándwich, multiplicar extremos por extremos. Seguido de esto, divide los términos semejantes para que se puedan contrarrestar.
Paso 4
Ya divididos los términos semejantes, en el denominador se pueden multiplicar los binomios. Y ese es el resultado final
Logaritmo con raíz y cociente
Paso 1
Aquí se aplican 3 reglas, la del cociente, la de la raíz, y la del logaritmo, por lo tanto, el primer paso es, derivar "u", copiar "v", colocar el signo -, copiar "u" y derivar "v", y todo eso se divide entre "v" al cuadrado. Después aplica la regla de la raíz, por lo que todo eso se divide entre 2 veces la raíz de "u" sobre la raíz de "v". Después se aplica la regla del logaritmo y por esto se copia la función de forma suspendía ya que no afecta en este primer paso.
Paso 2
Paso 3
Después aplicarás la ley del sándwich, multiplicando extremos por extremos ignorando la parte logarítmica "u" ésta se copiará sin alterar nada
Vuelve a aplicar la ley del sándwich, multiplicando extremos por extremos.
Multiplicar los términos semejantes y eliminar potencias con raíces en caso de que sean del mismo grado
Paso 6
Dividir los términos independientes del numerador y denominador
Paso 7
Contrarrestar los paréntesis con términos semejantes en el numerador y denominador, y dependiendo del resultado, el residuo, se queda arriba o abajo.
Paso 8
Por ultimo multiplica los binomios del denominador
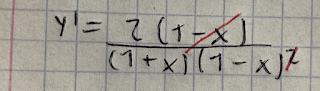
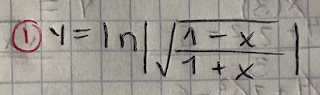
0 comentarios:
Publicar un comentario